AtCoder Heuristic Contestは、最近始まったAtCoderの定期コンテストで、最適解を出すのが難しい問題に対し、出来るだけ良い解を作成するコンテストです。 1週間程度の長期コンテストと、数時間程度の短期コンテストが交互に行われます。

今回のコンテストでは参加者1000人中5位と、非常にいい成績をとれました。システムテスト前の得点（コンテスト中に表示される暫定得点、100ケースの合計）は97,323,736,361(97.32G)点、システムテスト後の得点（3000ケース合計）は2,921,245,705,250(2.921T)点でした。

今回のコンテストでやったこと、やらなかったこと、考えたこと等をまとめます。

問題概要

30*30のグリッドグラフ上で、ジャッジが指定した2点間に対して最短経路を求めるクエリが1000回投げられます。しかし、各辺の長さは隠されており、自分のプログラムの返した経路の長さ（に0.9～1.1の範囲の一様乱数を掛けた値）のみを知ることができます。

得点は、各クエリに対して、真の最短経路aを自分のプログラムの返した経路の長さbで割った値a/bを、後半のクエリほど大きな重みを付けて和を取った値です。 1テストケースあたりの得点の上限がほぼ10⁹点になるように定数が掛けられています。

辺の重みの決定方法が若干特殊で、 $M$ というパラメータがテストケース毎にランダムで1か2になり、その値によって重みの付け方が異なります。また、 $D \in [100,2000$ ]というパラメータもテストケースごとに一つ生成されます。（これらの値を直接知ることはできません）

$M=1$ のとき

各行、各列ごとに、基準となる重みを $[1000+D,9000-D$ ]の範囲から一様ランダムに生成し、ここに各辺に対して $[-D,D$ ]の一様ランダムな値が加えられる。

$M=2$ のとき

各行、各列ごとに、基準となる重みを $[1000+D,9000-D$ ]の範囲から一様ランダムに二つ(ここでは $W_0, W_1$ とします)生成し、また、"切れ目"を1～28の範囲から一様ランダムに生成し、グリッドの片方の端から"切れ目"までを $W_0$ を基準、そこからもう片方の端までを $W_1$ を基準とし、ここに各辺に対して $[-D,D$ ]の一様ランダムな値が加えられる。

詳細についてはhttps://atcoder.jp/contests/ahc003/tasks/ahc003_aを参照。

自分の解法

ここからは時系列順にやったことを書いていきます。見出しの得点はpretest時の得点。

愚直解 (61.67G)

Submission #22782181 - AtCoder Heuristic Contest 003

まずは入出力が正しくできるか確かめるため、常にすべての辺の重みが一定であると仮定した状態で、毎回Dijkstra法で最短経路を求めるコードを書きました。

今回は提出コードをRustで書きましたが、proconioが内部のバッファリングの影響か、インタラクティブ環境でうまく動かなかったので、温かみのある入力パースを行いました。

勾配降下法の実装 (81.59G)

Submission #22784737 - AtCoder Heuristic Contest 003

$i$ 番目のクエリの応答の経路の長さ $y_i$ は、辺 $j$ の重みを $w_j$ 、その経路に含まれる辺の番号を $p_{i,1} , p_{i,2} , ... , p_{i,k_i}$ とすると、

$\displaystyle y_i = \sum_{j=0}^{k_i} w_{p_{i,j}}$

と書けます。ここで、行列 $A=(a_{ij})$ を $i$ 番目の経路に辺 $j$ が含まれていれば1、そうでなければ0として定義すると、

$\displaystyle \textbf {y} = A \textbf{x}$

と書くことができます。これを $\textbf{x}$ について解けば辺の重みが分かりますが、辺の数が1740あるのに対し、経路の数は高々1000個しかないため、一意な解は存在しません。また、帰ってくる経路長は乱数でスケーリングされているので、解が存在するとも限りません。

ここではとりあえず、辺の重みの近似値を、 $\textrm{min}(||A \textbf{x}- \textbf{y}|| _2)$ （最小二乗法）を勾配降下法によって求めることにしました。スケーリングは正規分布ではなく一様分布であるため、最小二乗法でいいのかという問題はありますが、とりあえず計算が簡単なのと、このあとCG法を使ってみようと思ったためこうしました。

勾配降下法の高速化、辺の重みの初期値の調整 (87.74G)

Submission #22785943 - AtCoder Heuristic Contest 003

雑に疎行列演算等を実装したところ、各クエリに対して20回しか勾配降下法のステップを回しただけで1200msほどかかっていたので、不要なメモリ確保をなくすなどの高速化をして、30ステップほど回すようにしました。また、未探索の辺を積極的に調べるため、未探索の辺の重みを期待値である5000よりも若干小さくしました。

高速化、学習率の調整 (92.19G)

同時に疎行列ベクトル積を高速化して、クエリごとに50ステップ程回せるようになりました。 get_unchecked (配列の境界チェックをせずに配列の要素にアクセスするunsafe関数)使ったら速くなった！（これでいいのか？）

もう少し1ステップで更新する大きさ（学習率）増やしても行けそうだったので、5倍(0.0001→0.0005)にしました。また、Dijkstra法は負辺/負閉路があるとまずいので、辺の重みを1000-9000の間になるようにclampした（Rust 1.42.0にはclampがなかったのでminとmaxで書いた）。

共役勾配法の導入 (92.83G)

二乗誤差の最小化 $\textrm{min}(||A \textbf{x}- \textbf{y}|| _2)$ は、実は方程式 $A^tA \textbf{x} = A^t \textbf{y}$ （正規方程式）を解くことによっても求められます。これは線型の連立方程式なので様々な方法で解けますが、行列サイズが1740*1740とかになるのでガウスの消去法等では計算量が大きすぎます。しかし、 $A$ はほとんどの要素が0の疎行列なので、これを生かした高速な求解アルゴリズムがいくつか存在します。ここでは共役勾配法（CG法）を使いました。

大きすぎる/小さすぎるweightの抑制(正規化) (93.15G)

辺の重みは1000-9000の間にありますが、経路長に誤差が乗っているため、方程式はその範囲外の値を解としてもってしまうことがあります。これを補正するために、 $|すべての辺の重みの平均-5000|$ も最小化対象になるように、行列 $A$ に入れました。さらに辺の重みの初期値をいじって93G点に乗せました。

重大な事実に気付く

ここまで初日の内容で、このときは1桁順位で満足していましたが、土日が明けた頃には40位程度まで落ちていました。で、上位の得点を見ると、すでに96G点台になっていました。この時点ではなんとまだ $M$ パラメータの存在に気付いておらず、1740辺に対し1000経路では明らかに情報が不足して、こんなに精度が出るのはおかしくないか？と思っていました。

何か勘違いとしているとまずい、ということで問題文やテストケースの生成方法をよく読むことにしました。すると、 $M$ というパラメータがあり、とくに $M=1$ の時は同じ行/同じ列の辺の重みはほとんど同じになっていることに（今さら）気付きました。たしかにこれを使えば大きくスコアを改善できそうです。

隣り合う辺の重みの差の抑制 (95.53G)

ということで、同じ行/列の辺であって、隣り合っているものについて、その重みの差を最小化対象に入れました。これは $A$ に片方の辺に $w$ 、もう片方の辺に $-w$ を掛けて足す行を追加すればよいです。

解と行列の使いまわし (96.85G)

いくらCG法が高速に収束するとはいえ、TLEしない10回程度の反復では、得られる解（辺の重み）の精度は限られています。そこで、辺の重みベクトルをクエリ間で使いまわすようにします。すると、前回得られた解からスタートするので、多くの場合今回求めるべき解の近くからスタートすることになり、収束が速くなります。また、これまでは行列やベクトルをクエリごとに再構築していたのを、使いまわすようにして高速化し、反復回数を増やせるようにしました。

この時点で暫定2位まで来ました。びっくりです。さすがに3日目まで問題文をよく読んでない人ばかりではないと思うので、おそらくCG法によって1740辺個別に重みを推定できるようになったのが大きく効いたのではないかと思います。

重みスケーリング (97.02G)

$M=2$ のときは、行中のどこかで辺の重みが一気に変わる場所が存在するはずで、このとき隣り合う辺の重みの差を抑制していると、真の重みから遠い重みを推定してしまいます。そこで、隣り合う辺の重みの差によるペナルティーがどれくらいかかっているかに応じて、ペナルティーを軽減したり増やしたりするようにしました。

パスの長さによる正規化 (97.13G)

これまで、各経路に対して、 $| \sum x_{i_j}-b_i|$ (と他の正規化項)の二乗和を最小化してきましたが、 $| \sum x_{i_j}-b_i|$ は経路中の辺の数が多いほど大きくなりやすいです。二乗和の最小化なので、この場合長い経路ほど頑張って誤差を最小化しようとすることになります。しかし、得られる経路の長さが真の値に対して0.9～1.1倍スケールされていることを考えると、短い経路の結果も長い経路の結果も同程度に重視すべきです。

そこで、経路中の辺の数 $n_i$ を用いて、 $|Σ(1/n_i)*x_{i_j}-b_i/n_i|$ (と他の正規化項)と正規化してやると、スコアが伸びました。

$M$ の推定、その他微調整 (97.32G)

$M=2$ かどうかをlossを見てアドホックに推定して、それに応じてペナルティーをいじるようにしました。あとは細かい改良を積み重ねたり、optunaでハイパーパラメータチューニングをしたりして、スコアを積み上げていきました。最後までM=2でDが小さいときに対するうまい対処法を思いつけなかったのが残念です。

解法そのものとは関係なくやったこと

複数テストケースを並列で走らせて、たくさんのテストケースについての得点を素早く集計する

問題の性質上、テストケースによって点数が大きくずれる、また、パラメータによって得点傾向が違うことから、少数のテストケースのみで変更点の有効性を確認するのは危険です。コンテスト中の提出は30分に一回しかできず、また、100ケースしかないため、かなり大きな改善でないと有効性を言えるほどの点差がつきません。さらに、改善が進むにつれ、一つの変更による得点の上昇が少なくなっていくので、その分テストケースの数を増やしていかないとテストケースに対して過学習を起こしやすくなります。

そのため、ローカルでたくさんのケースについて得点を集計する仕組みを構築しました。複数ノードにバイナリをばらまいて、各ノードで計算を走らせ、それを集計するスクリプトをRubyで書いて、コマンド一つでできるようにしました。最終的には家の計算機5台(Ryzen 7 Pro 4750GE * 4 + Ryzen 9 5950X * 1)の計48コア96スレッドで7680ケースについて回すようにしました。

性質上、並列度はテストケースの数だけ増やせるはずなので、次回の長期コンテストまでにはAWS Lambda等を用いて1000並列とかで回せるベンチマークシステムを構築したいです。

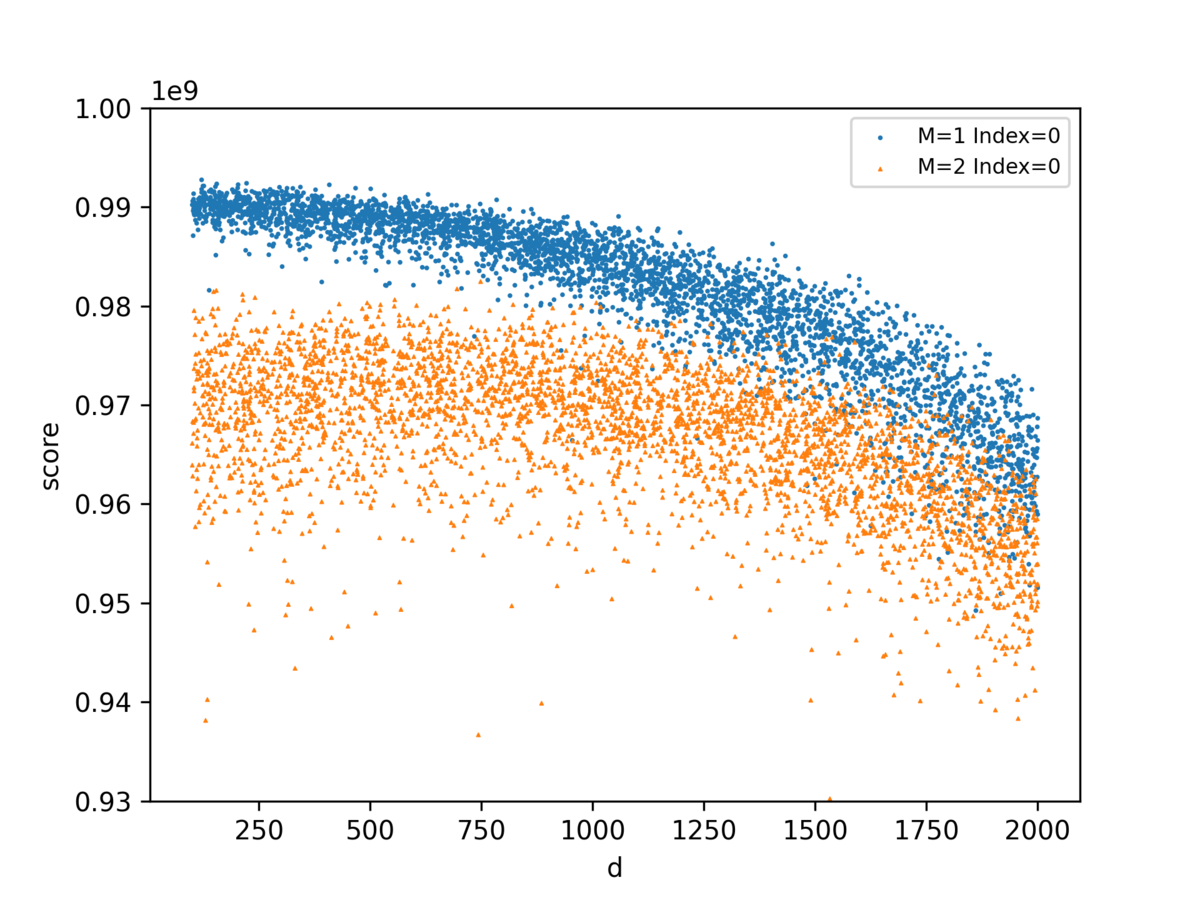
M,Dの値とスコアの関係をプロット

これも考察に大いに役立ちました。 $M=2$ のときだけでなく、 $D$ の大きいときもかなりスコアが下がっていることが確認できました。コードをいじった時にも、どういうところでスコアが改善・悪化しているかが見てわかるので良かったです。

optunaによるハイパーパラメータチューニング

使いどころが難しい（本質的な改善の方が大事）ですが、次のような場合に使ってとてもいい感じでした。

他のパラメータとの相対的な重みの大きさが変わるような変更の後

パスの長さによる正規化を実装したとき、経路に関するlossは（辺の数で割られるので）かなり小さくなります。それに応じて他の正規化パラメータの大きさも小さくする必要がありますが、複数パラメータ間のバランスをとるのは大変で、ここでoptunaで自動的にチューニングできたのはとても便利でした。

これから寝るとき

寝てるだけでスコアが良くなって便利。

もうできることが思い浮かばないとき

ボーっとしてるだけでスコアが良くなって便利。

計算機を温めたいとき

マイニングでもしとけ。

512ケース程度ではかなり過学習してしまうので、かなり計算資源が必要なのが難しいところだと思います。最初に128ケースまわしてとても悪そうだったらそこでやめて、悪くなさそうならもっとたくさんのケースを回す、とか工夫の余地はありそうです。

特に、今後クラウドで回そうとするならば、そのへんの計算量削減策を考えないとすぐにお金が融けていきそうです。

やったけどうまくいかなかったこと

隣接辺の重みの差をペナルティにするのではなく、ダミー辺との重みの差をペナルティにする

M=2のときに全然上手く行かなかった
M=1のときもスコアの分散が大きくなっただけであまり改善されず
辺ごとの重み推定を捨てて、行ごと(60変数や120変数/180変数のモデルにする)でやればよかったかも

経路の結果を正規化する際に、辺の数ではなくスコアで正規化

他のパラメータの重みもずらす必要があるのでoptunaで最適化もしたが、それでもだいぶ悪かった
経路長に乱数がかかった後の値がやってくるのがまずそう？

やっておけばよかったこと

$M,D$ の推定値によるモデルの切り替え

これをできなかったのは結構良くなかったな、という気持ち… M=2の時のモデルをどうするか、というのが本質的に難しそうですが… Dが大きいときには、わりとできることは少なそうで、ここの改善はあまり期待できなさそうです。

事前の環境整備

インフラ回り等、事前に準備できることは結構あるはずなので、そのへんを次回の長期コンまでにやっていきたいです。

感想

とてもよくできた問題だと感じました。これがM=3とかがあると、割と打つ手がなさそう（複雑度に比べて、得られる情報が少なすぎるため）で、かといってM=1だけだとすぐほぼ理論値までたどり着いてしまうはずで、この辺の塩梅が良かったように感じます。

結果にはとても満足していて、望外のいい結果を得られてとてもうれしいです。今後もいい結果を残せるように頑張ります。

prime's diary

そすうの日々を垂れ流しちゃうやつだよ

AtCoder Heuristic Contest 003で5位(2.921T点)を取りました